The felt experience of mathematics — witchcraft and black magic — “Shut up, kid!” — what is a real number? — shocked and embarrassed — a choir of angels singing — painting Cthulhu’s 👁️🗨️ third eye on the walls of our mathematics and science departments
Video from a monthly live Ask-Me-Anything!
The transcript is below. Plus: fun illustrations, and a wonderful comic strip, as mentioned in the video!
But first, how to join us next time:
It will be Sunday, January 26th, 9 a.m. Pacific Time. To participate, you need to subscribe (free or contributing), if you haven’t already:
You will also need the Substack mobile app (iOS or Android). If you have it open when the session begins, you’ll get a notification and a button to join:
It helps me a lot if you pose questions ahead of time, so I can prepare a bit! You could post them as comments here:
Or you can put them in the chat thread:
Transcript
The book Mathematica, by David Bessis
Big series of questions from
in the web chat, which I found fascinating because it connects with something that’s personally very important for me. His questions are, and observations concern, or are sparked by, a book called Mathematica by David Bessis.He began by asking if I’ve read that. I haven’t. A number of people have recommended it to me, and said “this is going to be relevant for you.” I read a bunch of reviews and boy, it sure is relevant for me! I gave a copy to my spouse
for their birthday, which was a couple weeks ago, and they’ve been reading it and raving about it. So I’m planning to borrow it when they’re done.Envisioning: the felt experience of mathematics
Tobin says, “Students of rationality often complain that the symbols on the page of rationality are impossibly dull and intimidating. Bessis says that that’s because we neglect to explain that there’s an associated living internal experience of imagination and intuition that is required to really understand and apply formal methods.”
Yes! Part Three of my meta-rationality book is supposed to go into this in a lot of detail. If you go to the metarationality.com site and find Part Three, which is called “Wielding the power of meaninglessness: Taking rationality seriously,” that has a sketch, currently only, of what I’m going to be saying about this.
For lack of a better word, I call this process of “imagination and intuition,” I call it “envisioning,” because it is similar to mental imagery, but it’s not the same. It has a kinesthetic component. There’s a wonderful piece by Terry Tao, who’s one of the greatest living mathematicians, about how when he was trying to understand a particular difficult piece of mathematics, he was rolling around on the floor, his whole body, feeling the effect of some mathematical function.
There’s a great quote from Einstein about this, where he says, um, it’s partly sort of visual, but it’s partly… propriostatic, proprio… that word! So you’re actually grabbing the mathematical objects, and you’re doing things with them.
Like most of my posts, this one is free. I do paywall some as a reminder that I deeply appreciate paying subscribers—some new each week—for your encouragement and support. It’s changed my writing from a surprisingly expensive hobby into a surprisingly remunerative hobby (but not yet a real income).
I’ve thought a lot about this. I was a math undergraduate. I saw people struggling with this. And for a lot of them, the problem was, and I found this really difficult myself. I got better at it. But translating between the symbols and the really felt experience of the mathematical dynamics, the objects in motion?
Tobin asked, “Is this part of meta-rationality?” I categorize it in the book as being part of what I call “advanced rationality.” Advanced rationality comes when your cookbook of methods that you were taught runs out, and you have to confront this situation without any definite method. And envisioning becomes particularly important at that point.
Envisioning is also really important in meta-rationality, but I think it’s not necessarily part of meta-rationality as I use that term.
Is the stage theory of development correct or necessary?
Tobin asks, “You tend to position meta-rationality as a discrete stage that comes after rationality. Must there be stages?”
This is an excellent question. This is controversial in the literature on this topic. I have a draft webpage about this. It’s fairly high priority. I want to get to it sooner rather than later.
This stage model is just a model. Like all models, formal and informal models, you have to apply it intelligently in a particular situation, and bear in mind that its applicability is always an imperfect fit; there’s some nebulosity. And be aware of the ways in which the model can mislead as well as illuminate. The stages aren’t really discrete, they do shade into each other, and whether they’re even meaningful for a particular purpose can vary.
Tobin says, “Or, can meta-rational thinking be incorporated into teaching and learning even when a student hasn’t yet mastered rational techniques?”
Well, I think full mastery is not necessary, but you need to have basic proficiency with a chunk of rationality before you could be meta-rational with regard to that chunk. And meta-rationality particularly comes into its own when either you’ve got a choice of rational systems you might apply; or you can’t find any, and you have to create a new one from scratch. So there’s some amount of proficiency with rationality that’s needed first, but certainly this envisioning thing is something I think we could and should be teaching much earlier and much more.
Mathematics is witchcraft and black magic
There’s a quote here from Mathematica:
The more I advanced, the further I dove into the heart of mathematics, the more I learned to master the techniques that facilitate deep understanding and creativity, the more it began to resemble witchcraft and black magic.
Well, here at this point, my ears prick up in a big way! Because I have practiced witchcraft in Wicca before I became a Buddhist, and black magic is a big part historically of Vajrayana, which is the style of Buddhism that I practice. I’ve got a whole website called Buddhism for Vampires, which is essentially about that, and it’s sparked by my horror at realizing that this very nice religion that I was practicing, which is all grounded on taking a vow to always benefit all sentient beings— how can black magic be a part of that? This is a big question. So I’ve got a website about it. And wow, this connects with mathematics?
Mathematica, the book, goes on:
Descartes thought that mathematicians guarded their secrets for fear of losing their prestige. The real explanation is undoubtedly more trivial. Mathematicians are simply afraid of being called insane.
I’ve got another explanation which I will suggest. I’m not sure about this, but if you admit that you’re doing black magic when you’re doing mathematics, maybe that could be a bit embarrassing or problematic. So, yeah!

“Bessis describes many truly great mathematicians who, when pushed in private, describe their methods in mystical terms: whispered by God, visited by spirits in dreams, communing with the universe, third eyes and sixth senses.” (Sixth sense is envisioning, I think!) “These ways of thinking produced undeniable results, and yet there isn’t a place in our current rationalist culture for that kind of language.”
Yes, I’m constantly down on rationalism for being an inadequate, incomplete, wrong story about how rationality works, and Part Three of the meta-rationality book is my alternative story about how mathematics works, and about how rationality works: science, engineering, mathematics.
“These are brilliant mathematicians with real results trying to tell us something about how their brains do rationality.”
Yes, it’s not what you get taught in the STEM curriculum, which teaches you rationalism, which is a basically religious theory of rationality, which is unhelpful. I observed this a lot. I did an undergraduate degree in mathematics and then I did a PhD in computer science; while I was doing that, I took a bunch of graduate level math courses. So I saw a lot. There’s my own experience of doing mathematics, and other STEM subjects. I went on and I did a lot of molecular biology, and then worked in a chemistry company. So I saw how people do rationality, and I have the experience of doing rationality, and the rationalist story is inadequate.
The taboo against talking about what mathematics is
With regard to math in particular, there is a very unhelpful taboo against talking about what it is like and how we do it. And I gather that’s what Bessis’ book is about. So I’m really excited to read that.
When I was a math undergraduate, I’d often put up my my hand to ask a question in class. I wasn’t trying to be difficult, but I’d ask, “What is this thing? What are we doing here? How does this work?” And the answer was always, basically, “Shut up, kid!” And my fellow math undergraduates weren’t willing to talk about it, really, either.
There’s a particular moment that I remember vividly, as a turning point for me. I was in an introductory analysis class, which… when you do calculus, the calculus class is all lies. The things they tell you aren’t true; they’re simplifications, which is good pedagogy. They’re directionally correct, but every single statement has… the reality is much more complicated. And the analysis class, you basically just go back over the whole of the calculus curriculum, and do it over again with fewer lies.

So it’s about real numbers, which is what calculus is mostly about. And I put up my hand, and the professor called on me, and I said, “So, uh, I don’t, um, what is a real number?” And the professor actually looked kind of shocked and flustered. And he paused for a minute to kind of collect himself, and then he said, “Well, if this was a foundations class, this is a sort of question we might address, but this isn’t, so we’re going to go on.”
I was like, “Well, hold on a moment. Um, I’ve had that answer before, a few times, and I kind of, I’m taking analysis because I thought this would tell me the foundations of calculus, that we would get real here and explain what was going on. And, um, but so apparently I need to take the foundations class. In this department, at this university, which is the foundations class?”
And then he looked shocked again. He said, “Well, maybe there’s something in the philosophy department… yeah, they don’t do one either. Um, you could go to Harvard, you could see if they have one.” (I was at MIT at the time, and MIT and Harvard students can take each other’s classes.) So he didn’t know where you could find out what a real number was. He probably didn’t know himself! He was shocked and embarrassed, and then hurriedly went on with what he wanted to say about whatever it was.
So I decided, at this point, I wasn’t going to get any answers. And I went to the library and dug around, and spent a couple of days there, and got the— Yeah!
says “Dedekind cuts.” I got the official answer, which satisfied me at the time. There’s two official stories about what real numbers are, which are Dedekind cuts and Cauchy sequences, which are really interesting! They’re also kind of wrong. And when people realized at the beginning, early 20th century, that this doesn’t actually work, there was a major crisis, and it kind of looked like mathematics might just completely fall apart. I’ve got a page on meaningness.com called “How rational certainty collapsed,” which is about what happened then.And the reality is, if you look for foundations for mathematics… People go into mathematics thinking they’re going to find absolute truth, and if you dig deep enough under those supposed absolute truths, you find it is clouds. There is no foundation other than clouds. It’s clouds all the way down. And I think a lot of mathematicians have read about this, and they realize there’s something scary there; and this is another part, probably, of why there’s a taboo about real talk about what math is, because it’s on sand, or clouds.
I’m ranting.
Blinding white light and angels
I’ll tell one more story, which is relevant to the mystical aspect.
This was some years later. I was in a graduate-level seminar on Kolmogorov complexity, which is, uh, you may have heard of Solomonoff induction. Kolmogorov complexity is essentially the same idea with a slightly different formalism. There’s a third version of it due to Gregory Chaitin. They all had more or less the same idea at the same time. This is fascinating stuff.
There’s a problem set, homework assignment, that had like five questions on it maybe, and the day before I had done problems one through four, which were not too difficult, and problem five I didn’t get done. And so I started in the morning working on problem five. I was working on that all day, nonstop. To do mathematics, you really need to focus, and if it’s a hard problem, you need to focus continuously, without interruption for long periods. So it was like late afternoon, early evening maybe. I hadn’t gotten anywhere. It was really frustrating.
And then suddenly I had, I received this insight. It was a really big deal. I actually can’t remember this. I think I was in the room that I shared with
, who’s in our session here now! Um, sitting at the desk there. I have the diary entry from it, which is all I know, but the diary entry said this insight came to me as blinding white light and a choir of angels singing. I think that must be metaphorical? I don’t think that was my literal experience, but it was the best I could do to communicate something that felt really important to me as a spiritual experience. And once I had this, I had to translate whatever this felt sense of the insight was into the symbols on the page that I could turn in as a homework assignment. But the experience was the thing.So I think we should talk about these things! You know, it’s sort of embarrassing to say “I had a mystical experience.” It makes it sound like it was a big deal, but it was just a homework assignment. I wasn’t proving anything new. I was being dumb. It shouldn’t have taken me all day to do this.
Let’s tell those taboo stories about mathematical experience!
Tobin asks “When thinking of someone such as a young scientist in the making, how can we help that person to make sense of such stories?”
Well, I think we should just tell them. I mean, you can find some of these stories. I’ve been collecting them to put into Part Three of the meta-rationality book, but they’re few and far between!
People are… it’s a taboo because it’s embarrassing. It’s like talking about your personal experience of sex. Several people said this to me. And, you know, I’m more willing to talk about my personal experience of sex than most people are. So I lack some kind of inhibition; that makes me willing to talk about math.
I think we should try and explain as best we can, even though these experiences are not very effable. They’re a little bit effable. I mean, just being able to say you have to translate between the symbols on the page and some kind of internal experience: that may be something that a lot of people are missing. When I saw people struggling with math, I think in a lot of cases it was because they didn’t know even that they should be making that translation, much less how. I don’t know how to teach how to do that, but I think we could try to draw our experience? We could paint it?
In a 2019 tweet thread, I asked how we can help each other break the code of silence. “A podcast series? A public, recorded virtual conference/workshop? A subreddit? A dedicated web site?”
That thread was a follow-on to this one, about the experience of “envisioning.” There were many interesting replies, too!
What is your experience of envisioning like? Or other felt experiences of doing rationality? Please leave a comment!
I think we all have the sense that we’re bad at it. There’s a passage from Richard Feynman, who was one of the greatest physicists of all time, and one of the ones who was most willing to talk about what it is like. Not very willing! But he’s got a passage where he talks about his experience of what I call “envisioning,” and he kind of dumps on himself. He says it’s “a kind of half-assed semi-vision thing.” And the “semi-vision” is right because it’s also “motoric.” There’s a passage from Einstein where he says it’s got this motor aspect to it, of moving things. But, you know, Feynman was embarrassed to talk about his experience of this! So, we should all admit to feeling, “Uh, you know, I’m embarrassed to talk about this because I don’t think I’m very good at it.”
And I felt like I didn’t quite have what it would take to become a professional mathematician. And I think that was partly a suspicion of “Yeah, I’m actually bad at that.” I was actually much better at the symbols on the page. I can do that. That makes me more like a computer scientist than like a mathematician.
So Tobin asked, “Can we embed those experiences in a kind of meta-rational understanding?”
Yes. Part Four of the meta-rationality book, which I’m struggling with now, is supposed to do that.
“Do we need to invent new, more polite terms for this kind of thing?”
I invented the word “envisioning,” because it’s a little more polite than “this half-assed, semi-vision-like thing.”
Rationality is embarrassing because it’s freaky! Not respectable!
“Or should we just use the old freaky ones?”
Well, let’s try both! We’re not talking about this at all. So we can talk about it lots of different ways and see what works for people.
“Should we paint third eye symbols on the brutalist walls of our mathematics and science departments?”
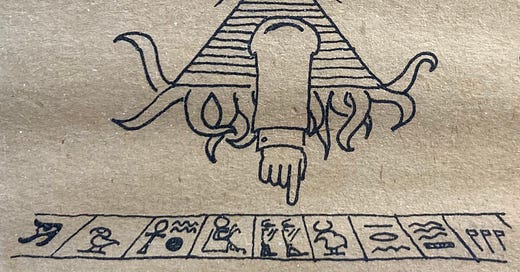
Yes! Let’s do that! I’m reminded of, again, in the undergraduate house that I shared with Mike Travers, who’s here now. There was a very talented artist who was our roommate also. We were in a four person room. He painted a comic, in which there was the third eye symbol, from a dollar bill, in a pyramid. And we were reading this book called Illuminatus!, which I’ve written a webpage about. I recommend it. It’s freaky! There’s the tentacles of Cthulhu along the bottom of the pyramid, and he had a hand coming out of the bottom of the pyramid, pointing at the tape of a Turing machine, with cabalistic symbols on the Turing machine tape. And I just loved this, and I wanted to paint it on the corridor wall of the MIT Artificial Intelligence Lab. I think it would have been fantastic. So yeah, let’s do that kind of thing.
Let’s make explicit that what we’re doing is freaky. Rationalism is all about trying to make rationality acceptable and respectable. And it really kind of isn’t.
The cartoon, by Dave Mankins
put me in touch with Dave Mankins, who drew the comic strip I exclaimed over in the video. It’s titled Mens et Manus, “mind and hand,” which is the official motto of MIT. Dave has kindly given me permission to reproduce it here, under the CC-BY-NC-SA license. It originally appeared in 1981 in Link, an MIT student newpaper we both wrote for. (Link was founded by our friend Brewster Kahle, who later founded the Internet Archive, sharing the same ideals.)
I hadn’t seen this in forty-three years! It’s just as fun as I remember it!





















Share this post